The Big O Notation

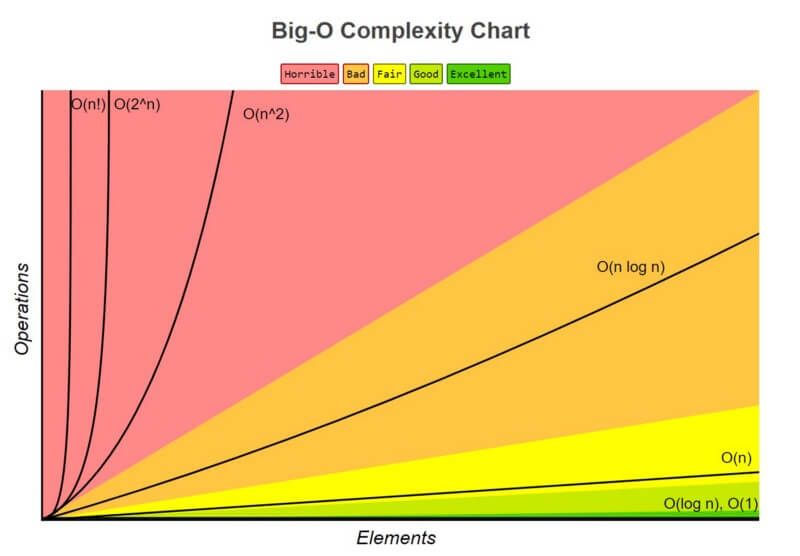
1. O(1)

void printFirstElementOfArray(int arr[]){printf("First element of array = %d",arr[0]);}

This function runs in O(1) time (or "constant time") relative to its input. The input array could be 1 item or 1,000 items, but this function would still just require one step.

2. O(log n)

3. O(n)

void printAllElementOfArray(int arr[], int size){for (int i = 0; i < size; i++){printf("%d\n", arr[i]);}}

This function runs in O(n) time (or "linear time"), where n is the number of items in the array. If the array has 10 items, we have to print 10 times. If it has 1000 items, we have to print 1000 times.

4. O(n^2)

void printAllPossibleOrderedPairs(int arr[], int size){for (int i = 0; i < size; i++){for (int j = 0; j < size; j++){printf("%d = %d\n", arr[i], arr[j]);}}}

Here we're nesting two loops. If our array has n items, our outer loop runs n times and our inner loop runs n times for each iteration of the outer loop, giving us n2 total prints. Thus this function runs in O(n2) time (or "quadratic time"). If the array has 10 items, we have to print 100 times. If it has 1000 items, we have to print 1000000 times.

5. O(2^n)

int fibonacci(int num){if (num <= 1) return num;return fibonacci(num - 2) + fibonacci(num - 1);}

An example of an O(2n) function is the recursive calculation of Fibonacci numbers. O(2n) denotes an algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2n) function is exponential - starting off very shallow, then rising meteorically.

6. O(n!)

Finally, one of the worst possibilities, factorial growth. The textbook example of this is the travelling salesman problem. If you have a bunch of cities of varying distance, how do you find the shortest possible route that goes between all of them and returns to the starting point? The brute force method would be to check the distance between every possible configuration between each city, which would be a factorial and quickly get out of hand.

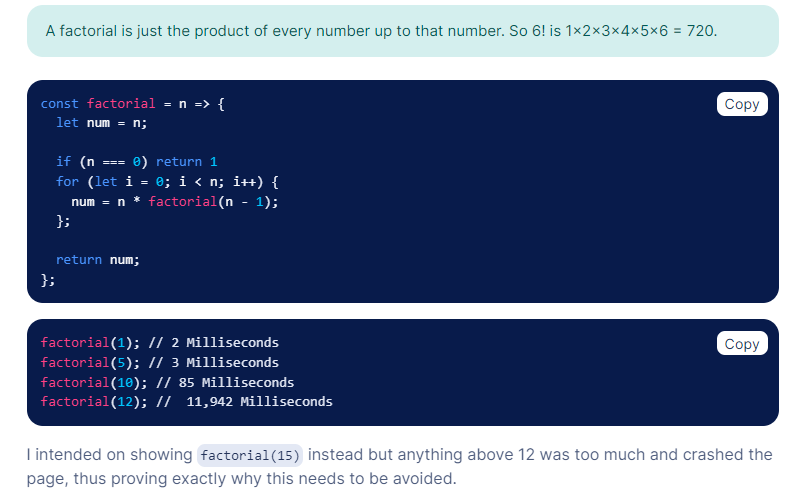
Since that problem gets very complicated very quickly, we’ll demonstrate this complexity with a short recursive function. This function will multiply a number by its own function taking in itself minus one. Every digit in our factorial will run its own function until it reaches 0, with each recursive layer adding its product to our original number. So 3 is multiplied by 2 that runs the function to be multiplied by 1 that runs it again to be stopped at 0, returning 6. Recursion gets confusing like this pretty easily.